在之前的文章中,我们讨论了如何使用抖动来通过打破量化误差和输入信号之间的统计相关性来提高理想量化器的性能。所谓理想,是指ADC传递函数具有统一的阶跃。换句话说,理想的ADC具有零DNL误差。这种抖动应用在需要高SFDR的无线电接收器中尤为重要。
在本文中,我们将讨论抖动的另一个重要应用,即改善现实中的A/D转换器的SFDR,例如AD6645,它会出现DNL误差。这种抖动应用在当今需要高SFDR的无线电接收器中尤为重要。
ADC静态和动态线性度在开始之前,让我们首先快速回顾一下提高ADC线性度的主要限制。尽管ADC使用不同的架构和电路实现,但它们有两个主要的非线性源:采样保持(S/H)电路和ADC的编码器部分。S/H非线性部分源于这样一个事实,即它具有有限的转换速率,并且当输入是具有大振幅的高频信号时,可能无法足够快地跟随输入。缺乏表现出足够转换率的S/H是许多ADC无法提供高于几兆赫信号带宽的高SFDR的一个关键原因。这也解释了为什么S/H的非线性与频率有关。S/H在确定ADC的动态(或AC)线性度方面起着关键作用。
另一个非线性源是ADC编码器部分。对于给定的ADC相位,编码器部分主要处理直流信号,因为它位于S/H之后。因此,编码器非线性会导致系统的静态(或直流)非线性。理想情况下,非线性成分不会随频率变化。静态非线性的特征在于ADC传递函数中的DNL和INL(积分非线性)误差。术语“静态非线性”可能用词不当,因为这种非线性成分不仅影响直流信号,而且在处理交流信号时还会降低线性度。
请注意哪种非线性类型占主导地位!传递函数非线性——确定性误差为了更好地理解静态非线性,我们将以图1所示的传递函数引入的非线性误差为例进行研究。

上图中的红色曲线表示非线性4位ADC,而蓝色曲线表示理想的4位响应。如果我们使用上述特性曲线将以4MHz采样的1.11kHz正弦波数字化,我们将获得图2中的波形。
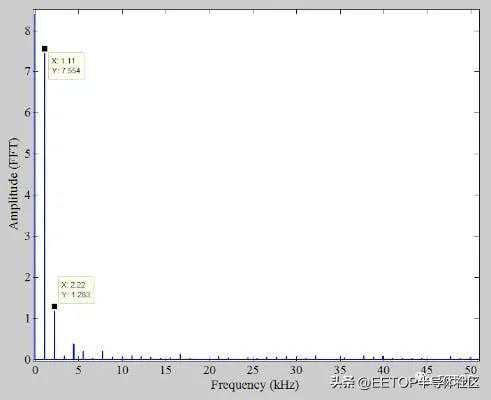
图2.以4MHz采样的数字化1.11kHz正弦波的波形
在图2中,绿色曲线显示输入,而蓝色和红色曲线分别是理想和非线性传递函数的输出。通过从红色曲线中减去蓝色曲线,我们可以确定非理想响应引入的非线性误差。这由图3中的红色曲线显示。
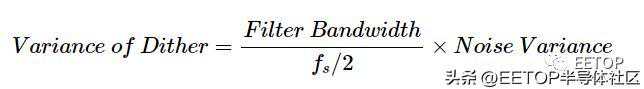
图3.显示非理想响应引入的非线性误差的图。
传递函数非线性引入的误差是确定性误差。这意味着,对于给定的输入电压,误差始终相同。例如,参考图1,我们观察到6LSB(最低有效位)的输入总是导致比理想值高3LSB的输出。这种确定性行为在输入和错误之间建立了相关性。如果输入处于特定频率,我们预计误差在与输入相关的某些特定频率处具有很强的频率分量。
图3可以帮助您更好地理解这种情况。在这种情况下,误差波形不完全是周期性的;但是,错误的整体形状似乎会以规律的方式重复出现。即输入信号在一个周期内有两次重复。这表明误差在输入的二次谐波处具有很强的分量。为了更好地形象化这一点,该图还绘制了2.22kHz(二次谐波)的正弦波。如您所见,正弦波近似于误差波形整体形状的趋势。
对非线性响应输出进行快速傅里叶变换(FFT),我们得到图4中的频谱,其中仅显示DC至50kHz范围。
图4.显示从DC到50kHz范围内的非线性响应输出FFT结果证实二次谐波是非线性响应的主要频率分量。值得一提的是,主要谐波分量的频率取决于ADC的INL形状。对于图1所示的非线性(有时称为弓形INL),二次谐波是主要谐波。对于S形INL,三次谐波是误差的主要频率分量。
打破ADC误差与输入之间的相关性如果我们向输入添加一个相对较大的随机信号,使ADC的整体输入以不可预测的方式在ADC传递函数的不同阶跃之间变化,我们可以在一定程度上减少确定性失真。这个概念如图5所示。
图5.显示ADC传递函数阶跃期间ADC输入变化的基本图。图片由AnalogDevices提供添加随机信号(或抖动信号)后,给定的输入并不总是转换为相同的输出电平。因此,即使输入不变,误差也会随时间变化。例如,考虑将6LSB的输入应用于图1中的传递函数。如果没有抖动,误差始终为3LSB。现在考虑抖动的情况。假设抖动信号偶尔等于2LSB。在2LSB处,非线性误差变为零。由于误差在0和3LSB之间变化,因此与未抖动情况相比,误差平均值有所降低。这个简单的例子展示了抖动如何消除输入和非线性误差之间的相关性,从而减少确定性失真。抖动通过使转换器的DNL误差离域或随机化来实现这一点。
通信系统抖动技术抖动技术在通信系统中特别有用。对于许多通信应用,输入可以是远低于ADC满量程的小信号。这个小信号使用相对少量的ADC输出码字。如果这些输出码字表现出较大的DNL误差,则输出将包含显著的谐波失真。
请注意,对于满量程(或大)信号,DNL误差在某种程度上是固有平均的。原因是大信号会覆盖ADC的所有输出码字。因此,当信号幅度降至低于满量程值20dB时,具有88dBFS满量程SFDR的ADC可能仅提供80dBFS的SFDR。在这种情况下,抖动技术可能有助于我们在低信号水平下保持ADC的SFDR性能。应该注意的是,由于输入电平很小,我们可以将抖动信号添加到输入,而不会过度驱动ADC。
ADC加入噪声——不是在丢失信息吗?你可能会问:我们在输入信号中加入比较大的噪声不是丢失了信息吗?答案是信息似乎在时域中丢失了。然而,通过适当选择噪声信号以及信号处理技术,我们可以重建原始信息。一种解决方案是减法式色抖动。在这种情况下,将图5中的基本图修改为下图(图6)。
图6.减法式抖动图。图片由AnalogDevices提供
在减法方法中,引入输入的噪声以相反的极性添加到输出,从而将系统输出端的净抖动噪声归零。在通信系统中使用的另一种有趣的技术是使用频率内容超出所需信号带宽的窄带噪声。几百kHz的小带宽对于抖动信号通常就足够了。带外噪声的两个可能位置是直流附近或略低于奈奎斯特频率(fs/2,其中fs是采样频率)。在可用于抖动目的的大多数通信系统中不使用这两个频率区之一。在这种情况下,可以很容易地在输出端滤除抖动。
分析一下我们假设的ADC让我们使用图1中的传递函数来研究这种技术。为此,我们向该ADC应用幅度为2LSB和DC值为7.5LSB的1.11kHz正弦波。这样的输入会执行ADC的中档代码。从略高于0Hz到30kHz范围的输出频谱如图7所示。
图7.1.11kHz正弦波的另一个示例图,其频谱范围略高于0Hz至30kHz对于这个特定的输入,有几个不同的谐波分量,但主要的仍然是二次谐波。将值转换为分贝,我们发现SFDR为17.47dBc。为了产生抖动信号,我们可以使用Matlab的“randn”函数来产生具有2LSBRMS(均方根)的宽带高斯噪声。应用以1.94MHz为中心的通带为100kHz的带通滤波器,宽带噪声被转换为略低于fs/2的窄带抖动。抖动信号的频谱如下图8所示。
图8.抖动信号的示例频谱由于抖动信号是原始噪声的带限版本,我们可以使用以下等式来确定抖动信号的方差:
代入数字,我们得到:
取该值的平方根,抖动信号的RMS为0.45LSB。抖动的峰峰值可以估计为6.60.45=2.97LSB(RMS高斯噪声乘以6.6转换为峰峰值)。请注意,抖动的峰峰值足够小,不会过度驱动ADC。应用抖动后,我们获得以下输出频谱(图9)。
图9.应用抖动RMS后的输出频谱可以看出,谐波被显著抑制。将值转换为分贝,我们获得27.9dBc的SFDR,与未抖动情况相比提高了10.43dB。抖动通过将信号杂散散布到本底噪声中来抑制谐波分量。
真实世界ADC的测试结果——ADC3424下面的图10显示了ADC3424对于70MHz输入的输出频谱。
图10.70MHz输入时ADC3424的输出频谱。图片由德州仪器提供ADC3424提供抖动功能作为内部特性。关闭内部抖动后,SFDR为91dBc。然而,随着内部抖动被激活,杂散扩散到本底噪声中,并且SFDR增加到99dBc。
抖动技术限制可显著改善ADCSFDR的适当抖动级别取决于特定ADC的架构和其他属性。SFDR的改善还取决于输入信号的幅度以及抖动的幅度。还应注意,超过一定的噪声水平,SFDR可能不会显著改善。以AnalogDevices的AD6645为例。该设备使用多级架构。对于这种类型的ADC架构,DNL误差具有重复模式,并且当输入扫过ADC输入范围时,DNL图中有一些尖峰。下面的图11显示了AD6645在其一小部分输入范围内的DNL图。
图11.AD6645在其一小部分输入范围内的DNL图。图片由AnalogDevices提供对于AD6645,尖峰每512个LSB出现一次。经实验发现适合此特定ADC的抖动电平为1024LSB峰峰值或155LSBRMS。应用更大的抖动不会显著改善AD6645的SFDR。对于这个ADC,抖动的峰峰值等于两个DNL尖峰之间代码距离的两倍。但是,我们不能断定这是所有多级ADC的一般规则。
推荐阅读:
PPT分享:SerDes专题--高速低抖动PLL/DLL/CDR电路专题
原创模拟IC论文分享--TCAS-II主编邀稿:极低抖动频率综合器的多速率时间戳建模
相位噪声vs时间抖动
计算隔离式精密高速DAQ的采样时钟抖动的简单步骤
深入浅出聊抖动(Jitter)
什么是抖动?利用抖动消除ADC量化误差