反相输入端电压是V-,同相输入端电压是V+,放大器输入的差分电压Vin为同相端输入电压与反相端输入电压之差,如式1-2。
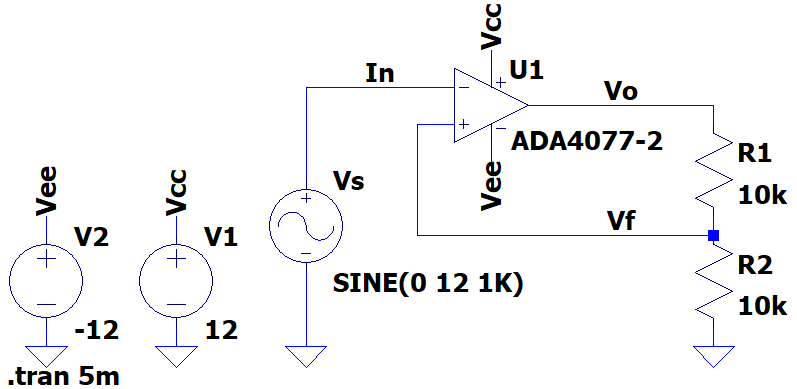
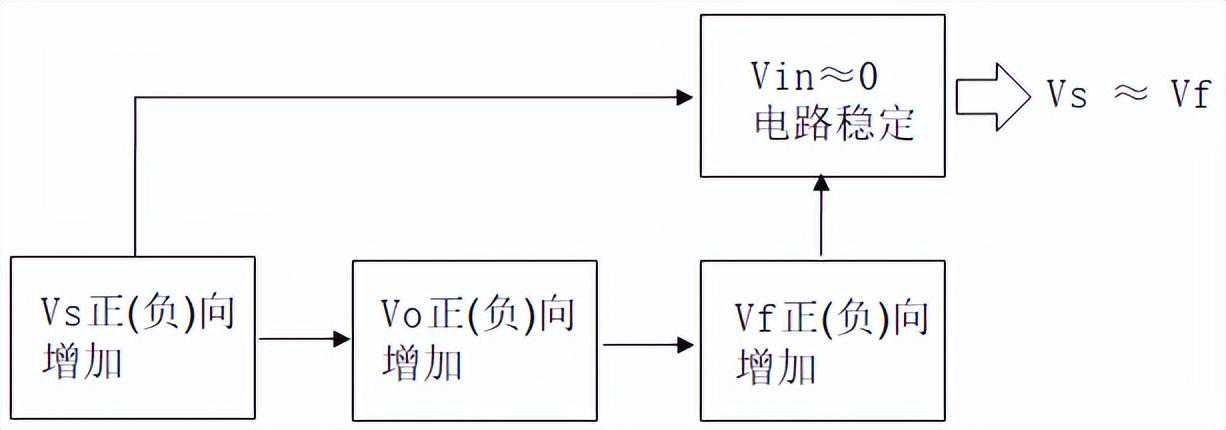
当放大器的供电电压为±Vcc,工作方式如图1.4,获得两点结论:
上限电压VU与下限电压VL的差值称为滞后电压VH。这个电压比较的工作过程是施密特触发器的工作原理。
图1.5施密特电路仿真图
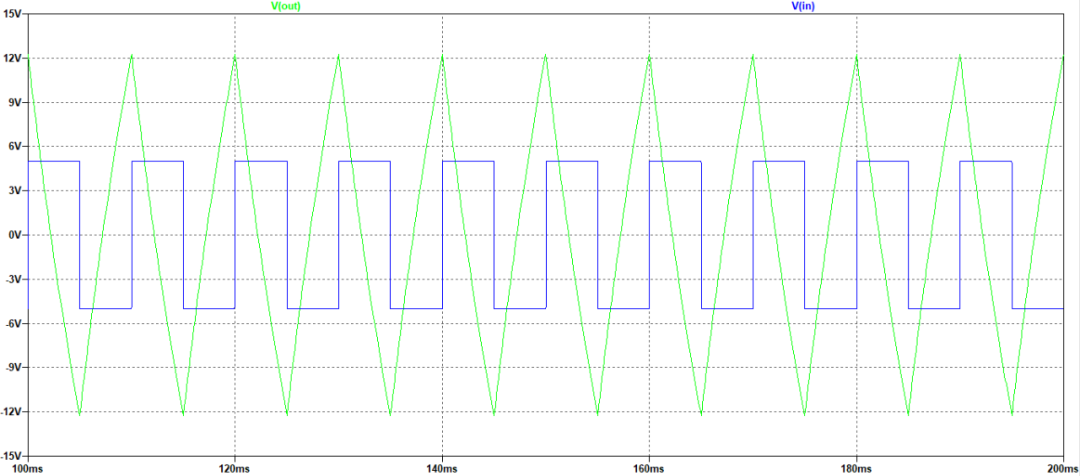
图1.6施密特电路仿真结果
“虚断”是指分别流入放大器两个输入端的电流I+,I-接近0A(由于偏置电流参数的存在,没有称为“真断”),即放大器的两个输入端与外部电路近似断开。
1反相放大电路
如图1.12(a)为双电源供电的反相放大电路,输入信号Vin,通过电阻Rg作用于放大器的反相输入端。由于“虚短”原则,反相输入端电压为0V,又由于“虚断”输入电流与输出电流大小相等,方向相反,即输出电压VO与输入电压Vin的符号相反,如式1-12。
反相电路的增益G,如式1-13
反相放大电路的力学模型是杠杆,如图1.12(b)。杠杆的支点是反相输入端的电压(0V),杠杆的长度是对应电阻(Rg、Rf)阻值,杠杆的摆幅是对应输入、输出的电压(VO、Vin)。
图1.12反相放大电路及力学模型
图1.13反相放大电路仿真图
电路瞬态分析结果如图1.14。输出(out)信号是频率为10KHz,峰峰值为1V正弦信号。峰峰值是输入信号的5倍,但是相位与输入信号相差半个周期。
图1.14反相放大电路仿真结果
上述是双电源供电电路,在单电源供电电路中,同相输入端的“地”电位将由参考电压Vref取代,典型取值为电源电压的一半,如图1.15。因此,输入电压和输出电压将以Vref电压为参考,其输入电压与输出电压关系满足式1-14。
图1.15单电源供电反向放大电路
2同相放大电路
如图1.16(a),双电源供电的同相放大电路,输入信号Vin直接作用于放大器的同相输入端。由于“虚短”原则,反相输入端电压为Vin,再根据“虚断”原则输入电流与输出电流大小相等,方向相同,即输出信号VO与输入信号Vin符号相同,如式1-15。
整理得到同相电路的增益G,如式1-16。
同相放大电路的力学模型是钟摆,如图1.16(b)。钟摆的固定点是地,上摆(Rg)的摆幅Vin,带动下摆(Rg+Rf)产生Vo的摆幅VO,下摆(VO)的方向跟随上摆(Vin)的方向。
图1.16同相放大电路及力学模型
图1.17同相放大电路仿真图
电路瞬态分析的结果如图1.18。输出信号是峰峰值为4V的正弦信号,是输入信号幅值的2倍,并且与输入信号同频率、同相位。
图1.18同相放大电路仿真结果
3求和电路
如图1.19为双电源供电的求和电路,在反向放大电路基础上增加Vin2、Vin3两路信号源,分别通过Rg2、Rg3连接到反向输入端。根据叠加定律电路,输出信号是输入信号Vin1、Vin2、Vin3单独作用时,产生的输出信号Vo1、Vo2、Vo3的总和,如式1-17。
图1.19求和电路
图1.20求和电路仿真图
电路瞬态分析的结果如图1.21。输出信号的峰峰值为6V,是将Vin1峰峰值放大2倍、Vin2峰峰值放大5倍,Vin3峰峰值放大1倍的总和,输出信号频率与输入信号频率相同,输出信号相位与输入信号相位相差半个周期。
图1.21求和电路仿真结果
4积分电路
如图1.22为双电源供电的积分电路,输入端电流Iin,如式1-18。
输出端电容上的蓄积电压VO,如式1-19。
又因为电容Cf电荷量满足式1-20。
图1.22积分电路
根据“虚短、虚断”原则,输出信号VO为输入信号Vin积分后的电压,如式1-21。
图1.23实用积分电路
图1.24积分电路仿真图
电路瞬态分析的结果如图1.25,输出信号为锯齿波,是对输入信号的连续积分运算。
图1.25积分电路瞬态分析结果
5微分电路
如图1.26为双电源供电的微分电路,输入信号Vin,如式1-22。
将式1-22对时间t求导数,整理获得输入电流Iin,如式1-23。
根据“虚短、虚断”原则,输出电压VO满足式1-24。
图1.26微分电路
图1.27实用微分电路
图1.28微分电路仿真图
电路瞬态分析的结果如图1.29,在输入信号电平转换时进行微分运算产生输出脉冲信号。
图1.29微分电路仿真瞬态分析结果
6差动放大电路
由“虚短”原则,放大器反相、同相端输入电压Va、Vb,如式1-25。
根据“虚断”原则与基尔霍夫定律可得In1等于Io,如式1-26。
进一步整理可得,式1-27。
当Rg2=Rg1,Rf=Rref时,式1-27可简化为式1-28。
图1.30差动放大电路
图1.31差动放大电路仿真图
电路瞬态分析的结果如图1.32,输出信号是峰峰值为3V,频率为10KHz的正弦波。幅值是将输入信号Vin1,Vin2的差值放大10倍。输出信号与输入信号的频率相同,相位相差半个周期。
图1.32差动放大电路瞬态仿真结果